If the above figure makes you nostalgic, I’m certain that you’ve played the Binary sudoku before! Remember the last pages of your school notebooks? Those days were fun, weren’t they?

Binary is the underpinning of current computer technology. The binary number system plays a huge role in the process of  ‘Digital Encoding.’ Thus the Binary Numbers play a huge role in connecting people all around the world through computers.

This blog post will help you explore Binary numbers. Here is the table of contents. You can jump to any of the topics directly.

Table of contents

• Binary Numbers – Beginner’s Guide
• Overview of Base 10 System or Decimal System
• Binary number system
• Decimal number system
• Binary to Decimal Conversions
• Decimal to Binary Conversions
• What Are Hexadecimal Numbers?
• Hexadecimal number system
• Examples of Hexadecimal Numbers & its conversions
• Conclusion

Overview of Base 10 System or Decimal System

The base 10 system is also known as the Decimal system. Base-10 is used in most modern civilizations and was also common for ancient civilizations, most likely because humans have 10 fingers!

A decimal is any number in our base-ten number system. The decimal point is used to separate the ones place from the tenths place in decimals. As we move to the right of the decimal point, each number place is divided by 10. When reading decimals, the decimal point should be read as “and.” Thus, we read the decimal 57.49 as “fifty-seven and forty-nine hundredths.

With the advent of e-technology binary systems emerged as a counting system to communicate with computers. It has a wide range of applications in the real world. Let’s explore how the binary system works.

Let’s get started!

Binary number system

• The binary number system uses only two digits: 0 and 1.
• Thus, the numbers in this system have a base 2.
• 0 and 1 are called bits.
• 8 bits together make a byte.
• The data in computers is stored in the form of bits and bytes.

Examples: 1011₂, 1001001₂,111_2, etc.

Application: The binary number system is used in computer technology. All computer languages and programs are based on the 2-digit number system used in digital encoding ( the process of representing data as discrete bits of information).

Decimal number system

• The decimal number system uses ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
• Thus, the numbers in this system have a base of 10.
• If we see a number without a base, it means that its base is 10.
• This is the system that we generally use to represent numbers in real life.

Examples: 18₁₀, 222₁₀, 467₁₀, 7877₁₀

Applications:  We use decimals everyday when dealing with money, weight, length, etc. Decimal numbers are used in situations where more precision is required than the whole numbers can provide.

Binary to Decimal Conversions

Multiply each digit of the given number, starting from the rightmost digit, with the exponents of the base 2, where the exponents start from 0 and increase by 1 every time. Then just add the above products.

Let’s try an example.

Example:

Convert 1000010₂ to the decimal system.

Solution:

Starting from the rightmost digit, we multiply each digit with the corresponding powers of 2. Let’s start.

Adding all the numbers, we get 0+2+0+0+0+0+64 = 66

Pictorially,

Thus,

1000010₂ = 66₁₀

Decimal to Binary Conversions

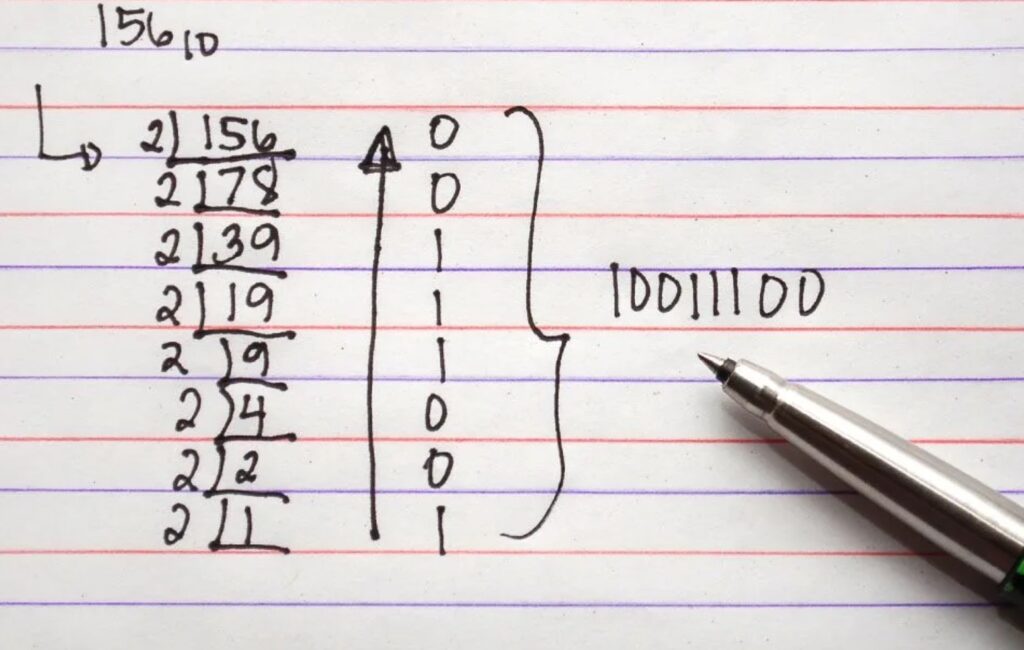
Divide the given number by the base of the required number and note down the quotient and the remainder in the “quotient-remainder” form repetitively until we get the quotient to be less than the base. The new number in the required number system is obtained just by reading all the remainders and the last quotient from bottom to top.

Let’s try an example.

Example:

Convert 999₁₀ to binary system.

Solution:

Reading all the remainders along with the last quotient from bottom to top we get the required conversion.

Thus,

999₁₀ = 1111100111₂

What Are Hexadecimal Numbers?

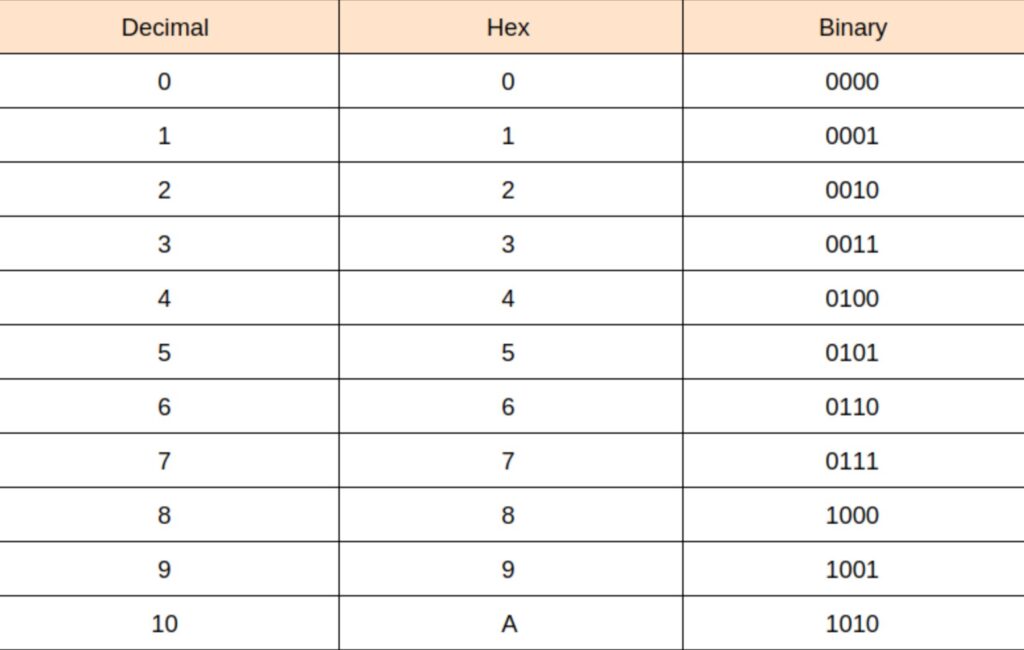
Hexadecimal number system

• The hexadecimal number system uses sixteen digits/alphabets: The digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, and the alphabets A, B, C, D, E, and F.
• Thus, the numbers in this system have a base of 16.
• Here, A−F of the hexadecimal system indicates the numbers 10−15 of the decimal number system, respectively.
• This system is used in computers to reduce the large-sized strings of the binary system.

Examples: A7B₁₆, BC_16, etc.

Applications: A computer can understand positional number systems where there are only a few symbols called digits, and these symbols represent different values depending on the position they occupy in the number. Computers are usually designed to process hexadecimal numbers.

Examples of Hexadecimal Numbers & its conversions

Example 1:

Convert 16F80E₁₆ into the binary system.

Solution:

Conversion of 16F80E₁₆ to decimal: Multiply each digit with corresponding powers of 16, starting from the rightmost digit.

Adding all the numbers, we get  14+0+2048+61440+393216+1048576 = 1505294

So 16F80E₁₆ = 1505294₁₀

Conversion of 1505294₁₀ to binary:

Reading all the remainders along with the last quotient from bottom to top, we get the required conversion.

Thus,

1505294₁₀ = 101101111100000001110₂

Hence, 16F80E₁₆ = 101101111100000001110₂

Example 2:

Convert 100011₂  into the hexadecimal system.

Solution:

To convert a binary into a hexadecimal number first, we have to convert the binary into decimal and then from decimal to hexadecimal.

Conversion of 100011₂ to decimal: Multiply each digit with corresponding powers of 2, starting from the rightmost digit.

Adding all the numbers, we get  1+2+32 = 35

So, 100011₂ = 35₁₀

Conversion of 35₁₀ to hexadecimal:

Reading all the remainders along with the last quotient from bottom to top, we get the required conversion.

Thus,

35₁₀ = 23₁₆

Hence, 100011₂ = 23₁₆

Conclusion

Binary numbers are very important in this digital world of computers. They help in the field of data analytics, data structure algorithms, and computer architecture. I hope you enjoyed reading this article. You can share your thoughts by commenting down below.

Also, you can learn all about numbers at Cuemath by just clicking here. This is one of the leading Math platforms which makes Math super easy and fun! Students can learn at their own pace through various learning tools like Numeric puzzles, worksheets, tab exercises, puzzles, math boxes, and much more. And in case you want to build some math muscles.

If you have any queries, comment down below, we will shortly get back to you. Thank you for spending your valuable time here. I hope it was a good read.